「線段相交與否」與「球體碰撞點」
最近在實作 Delaunay Triangulation 時,遇到需要刪除交叉線斷的問題,才想到之前碩論在做撞球的時候也有解決到類似的問題,但忘記怎麼解了,趕緊複習了一下,並想在這記錄下來,日後好再回來查找。
線段相交與否
要求線段 AB 與 線段 CD 是否相交,可以嘗試以下兩種方法。
方法一:解連立求 x
最直觀的方法,把方程式列出來後解連立。
f(x) = Mab * x + (A.y - A.x * Mab)
f(x) = Mcd * x + (C.y - C.x * Mcd)其中 Mab 是 AB 的斜率, Mcd 是 CD 的斜率。
Mab = (B.y - A.y) / (B.x - A.x)
Mcd = (D.y - C.y) / (D.x - C.x)連立解完會長成下面這樣:
x = ((C.y - C.x * Mcd) - (A.y - A.x * Mab)) / (Mab - Mcd)最後在比較 x 的範圍有沒有超出 AB 的 x 與 cd 的 x 即可。
方法二:外積
本方法參考自:https://bryceboe.com/2006/10/23/line-segment-intersection-algorithm/
當兩線斷相交時,A 和 B 會被 CD 分開, C 和 D 會和 AB 分開。
你可以仔細觀察一下此時弱勢使用 CD 分開 A 和 B,並組成 CDA 和 CDB 這兩個三角形。其轉向一定是相反的。
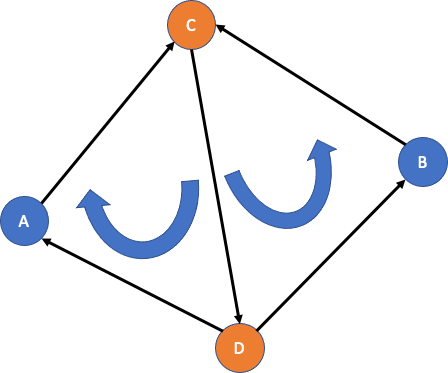
同理,若是我們是用 AB 把 C 和 D 分開,也是一樣:
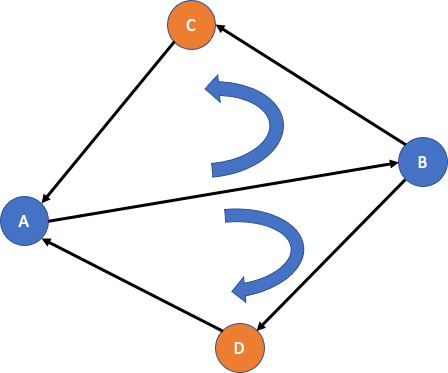
因此,我們要先有一個確認轉向的 Function:
// 3D
bool ccw(Vector3 A, Vector3 B, Vector3 C, Vector3 normal)
{
return Vector3.Dot(Vector3.Cross(A - B, C - B), normal) > 0);
}// 2D
bool ccw(Vector2 A, Vector2 B, Vector2 C)
{
Vector2 BA = A - B;
Vector2 BC = C - B;
return BA.x * BC.y - BA.y * BC.x > 0;
}
上述式子中簡單來說,若兩向量外在 XY 平面且是逆時針,外積後得到向量必定會指向正 Z 軸。因此以 2D 的式子來說,我們直接算行列式就是外積後向量中的 Z 的量,若大於 0 即是指向正 Z,以 3D 的世子來說,若在 XY 平面上, normal 給 (0, 0, 1) 即可,若不在 XY 平面上,就需要改自己的 normal 向量。
有了 ccw 這個 Function 後,我們就只要確認 ccw(A, B, C)與ccw(A, B, D)相反,ccw(C, D, A)與ccw(C, D, B) 相反即可。
bool CheckIntersection(Vector3 A, Vector3 B, Vector3 C, Vector3 D)
{
return ccw(A, B, C) != ccw(A, B, D) && ccw(C, D, A) != ccw(C, D, B);
}球體碰撞點
求球體碰撞點的方法與求線段相交很像,但又不太一樣,首先我們先改成用起始點和速度的方式來表達。
o1: ball1 的起始點
v1: ball1 的速度o2: ball2 的起始點
v1: ball2 的速度f1(t) = o1 + v1 * t (ball1 的路徑)
f2(t) = o2 + v2 * t (ball2 的路徑)
接下來請看下圖,因為我們要假設兩求相撞,因此在相撞時,兩求的距離一定是剩下 2r (兩倍的球半徑)。
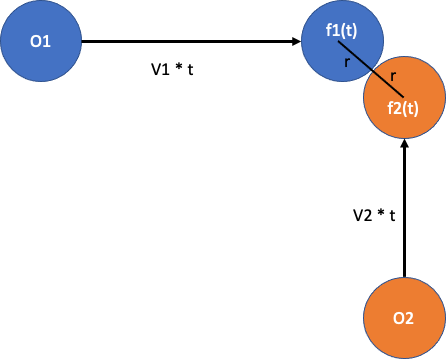
因此我們可以列出下列式子:
|f1(t) - f2(t)| = 2r
=> |f1(t) - f2(t)|² = (2r)²
=> |o1 + v1t - o2 - v2t|² = 4r²
=> |(o1 - o2) + (v1 - v2)t|² = 4r²以下為了方便運算,我把 o1 — o2 定義為 Δo ,v1 — v2 定義為 Δv 。
=> |Δo + tΔv|² = 4r²
=> |Δv|²t² + 2t(Δo⋅Δv) + |Δo|² = 4r²
=> |Δv|²t² + 2t(Δo⋅Δv) + (|Δo|² - 4r²) = 0求到此處,一元二次方程式就出現了,接下來用公式解求兩根即可,因此我們要先簡化算是,找出 A, B, C 三個係數。
A = |Δv|²
B = 2(Δo⋅Δv)
C = |Δo|² - 4r²不過在帶入公式解前先帶入判變式看看有沒有有理根:
判別式:
Δ = B² - 4AC > 0公式解
t = (-B ± √Δ) / 2A
若判別式不成立就代表兩球不會碰撞,可能是錯過或是本來就平行之類的;另外若是 v 採用的不是速度而是距離,當 t > 1 時則代表焦點超出距離,這種判別方式是被我用在逐幀計算時,用來計算是否在此幀碰撞到,我會先用速度 * deltaTime 後算出球的移動距離內有沒有碰撞可能,若 t > 1 代表是在未來的幀才會碰撞。


留言
張貼留言